Variational Inference

Motivation

VAE 기반 추천 시스템 (Variational Autoencoder for Collaborative Filtering) 에서

x: 유저의 시청 기록 = [1, 0, 0, 1, 1, 0, ...] (영화 클릭 여부 벡터)
z: 유저의 잠재 성향/임베딩 (ex. 로맨스를 좋아함, 액션은 별로 안 좋아함)

유저가 어떤 잠재 변수를 가졌는 지 알면, 비슷한 분포의 유저에게 같은 영화를 추천해 줄 수 있다! 즉, $p(z \mid x)$ 를 구해야 한다. 하지만, $p(z\mid x)$ 를 직접 구하는 것은 매우 어렵다.

$p(z \mid x) = \frac{p(x, z)}{p(x)}$ 인데, $p(x) = \int p(x, z) dz$ $p(x)$ 는 intractable

MCMC를 사용하면 해결되긴 하지만, 속도가 너무 느림

Idea

posterior 분포 $p(z \mid x)$ 를 적당히 근사할 수 있는 분포 $q(z)$ 로 대체해서 복잡한 계산을 없애자.

여기서 $q(z)$ 는 우리가 다루기 쉬운 분포를 사용하자. ex. gaussian, GMM, beta 등
분포의 파라미터(ex. $\mu, \sigma$ )를 적당히 바꿔가면서 $p(z \mid x)$ 랑 가장 유사해지는 분포를 찾자.

$q(z) \approx p(z\mid x)$ 가 되게끔 KL divergence를 최소화하는 방법으로 구할 수 있다.

$q^*(z) = \arg \min_q \, \text{KL}(q(z) \,\|\, p(z\mid x))$

여기서, ELBO를 최대화 하는 방법으로 KL을 divergence를 최소화 할 수 있다.

KL divergecne의 정의에 의해,

\begin{aligned} D_{\text{KL}}(q(z) \parallel p(z \mid x)) &= \mathbb{E}_{q(z)} \left[ \log \frac{q(z)}{p(z \mid x)} \right] \\ &= \mathbb{E}_{q(z)} \left[ \log q(z) - \log p(x, z) + \log p(x) \right] \\ &= \mathbb{E}_{q(z)} \left[ \log q(z) - \log p(x, z) \right] + \log p(x) \\ \end{aligned}

따라서,

\log p(x) = \mathbb{E}{q(z)} \left[ \log p(x, z) - \log q(z) \right] + D{\text{KL}}(q(z) \parallel p(z|x))

\log p(x) = \mathcal{L}(q) + D_{\text{KL}}(q(z) \parallel p(z|x))

ELBO는 다시, 다음과 같이 나타낼 수 있다.

\mathcal{L}(q) = \mathbb{E}_{q(z)}\left[ \log \frac{p(x, z)}{q(z)} \right]

\log \frac{p(x, z)}{q(z)} = \log \frac{p(x \mid z)p(z)}{q(z)} = \log p(x \mid z) + \log \frac{p(z)}{q(z)}

\begin{aligned} \mathcal{L}(q) &= \mathbb{E}_{q(z)} \left[ \log p(x \mid z) + \log \frac{p(z)}{q(z)} \right] \\ &= \mathbb{E}{q(z)}[\log p(x \mid z)] + \mathbb{E}{q(z)}\left[\log \frac{p(z)}{q(z)}\right] \end{aligned}

\mathcal{L}(q) = \mathbb{E}{q(z)}[\log p(x \mid z)] - D{\text{KL}}(q(z) \parallel p(z))

첫 번째 항은 “잠재 변수 z가 분포 q(z)를 따른다고 가정할 때, z로부터 x를 설명하는 로그확률의 평균”을 의미한다.

두 번째 항은 **잠재 변수 $z$ **가 인코더 $q(z \mid x)$ 에서 너무 “마음대로” 분포를 갖지 않도록 **사전 분포 p(z)**에 가깝게 유도하는 정규화(regularization) 역할을 한다.

ELBO 최대화

$argmax_q ELBO = argmax_q E[logp(x \mid z) + logp(z)] - E[logq(z)]$

여기서 q는 다변량 함수이다. 변수들 간 correlation이 존재하고 서로 다른 분포의 joint를 구하는 것은 매우 어렵다.

MFVI (Mean Field Variational Inference)

분포간의 correlation을 모두 무시하고, 변수들을 독립적으로 근사하자.

$q(z) = \prod_{j=1}^{J} q_j(z_j)$

$ELBO = -KL[q_j \mid \exp(\mathbb{E}_{i \ne j}[\log p(x, z)])] + C$

따라서, KL divergence를 최대화 하기 위해선,

$q_j(z_j) \propto \exp \left( \mathbb{E}_{i \ne j}[\log p(x, z)] \right)$

확률 분포로 만들기 위해 아래처럼 **정규화(normalizing constant)**를 붙여준다.

$q_j(z_j) = \frac{\exp(\mathbb{E}{i \ne j}[\log p(x, z)])}{\int \exp(\mathbb{E}{i \ne j}[\log p(x, z)]) dz_j}$

각 $j$ 에 대해:

다른 모든 $q_i$ 를 고정
$q_j$ 만 업데이트
1, 2의 과정을 ELBO가 수렴할 때까지 반복한다.

Monte Calro Approximation

기대값을 계산할 수 없을 때, 샘플링을 통해 근사하는 방법

Motivation

어떤 확률분포 $p(\theta)$ 아래에서, 어떤 함수 $f(\theta)$ 의 평균을 알고 싶은 상황.

$\mathbb{E}_{p}[\theta] = \int \theta \cdot p(\theta) \, d\theta$ 이런 형태의 계산은 머신러닝, 베이지안 추론, 강화학습 등에서 자주 등장한다.

Idea

적분 대신 샘플 몇 개 뽑아서 평균을 내자.

$\mathbb{E}{q(z)}[\log p(x|z)] \approx \frac{1}{L} \sum_{l=1}^{L} \log p(x \mid z^{(l)}), \quad z^{(l)} \sim q(z)$

$z$ 를 $q(z \mid x)$ 에서 샘플링한다.
디코더 $p(x \mid z)$ 에 넣는다.
log likelihood 계산한다.

보통 $L = 1 \sim 5$ 정도만 해도 잘 작동한다.

Sampling

Inverse CDF

특정 분포를 샘플링 하기 위해서, $z \sim Uniform(0,1)$ 의 z를 transformation을 통해 우리가 원하는 분포로 옮겨주자. 원하는 분포 T는 어떻게 찾을 수 있을까?

$T(z) = X$ 가 되도록 하는 $T$ 를 찾아보자.

$F_X(x) = p(X\geq x) = p(T(z)\geq x) = p(z \geq T^{-1}(x)) = T^{-1}(x)$

$F_X(x) = T^{-1}(x)$

$T(x) = F_X^{-1}(x)$

분포가 복잡할 때, Inverse CDF를 구하기 어렵다는 단점이 있다.

Rejection Sampling

우리가 샘플링하고 싶은 분포:

$p(z) = \frac{1}{Z_p} \tilde{p}(z)$

$\tilde{p}(z)$ : unnormalized density (비정규화 상태)
$Z_p$ : 정규화 상수 (보통 모름)
이런 상황에서는 Rejection Sampling을 사용한다.

Proposal 분포 $q(z)$ 와 scaling factor $k$ 를 사용해 $kq(z) \geq \tilde{p}(z)$ 가 되는 범위를 덮도록 한다.

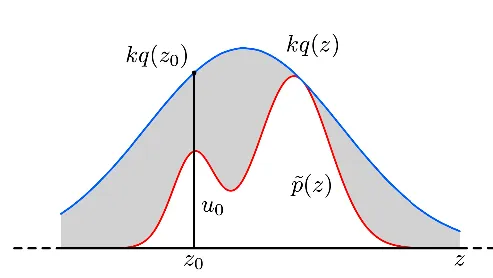
$z_0 \sim q(z)$ 에서 샘플링
$u_0 \sim \text{Uniform}(0, kq(z_0))$ .
$u_0 \leq \tilde{p}(z_0)$ 이면 accept, 아니면 reject

accept될 확률: $p(\text{accept}) = \int \frac{\tilde{p}(z)}{kq(z)} q(z) dz = \frac{1}{k} \int \tilde{p}(z) dz$

수식 유도

p(\text{accept} \mid z) = \int_0^{\tilde{p}(z)/kq(z)} \frac{1}{kq(z)} du = \frac{\tilde{p}(z)}{kq(z)}

q(z) p(\text{accept} \mid z) = \frac{\tilde{p}(z)}{k}

kp(\text{accept}) = \int \tilde{p}(z) dz = Z_p

p(z) = \frac{\tilde{p}(z)}{Z_p} = \frac{q(z) \cdot p(\text{accept} \mid z)}{p(\text{accept})}

→ rejection sampling을 통해 $p(z)$ 에서 제대로 샘플링한 것과 같아진다!

단점
- 고차원에서는 $k$ 를 매우 크게 잡아야 함
- reject 비율이 커지고, 학습이 느려짐
- → 고차원에선 비효율적이다

Importance Sampling

기대값이 알고싶을 때 사용, 기대값 근사.

$E[f] = \int f(z)p(z)dz \rightarrow E[f] \approx \sum^L_{l=1}p(z^{(l)})f(z^{(l)})$

E(f) = \int f(z)\frac{p(z)}{q(z)}q(z)dz \rightarrow E[f] \approx \frac{1}{L}\sum^{L}_{l=1}\frac{p(z^{(l)})}{q(z^{(l)})}f(z^{(l)})

proposal $q(z)$ 가정. $q(z)$ 에서 sampling

$\tilde{p}(z)$ 와 $\tilde{q}(z)$ 를 통해 구할 수 있다. 상수배 한 비율만 구할 수 있음. $\tilde{r_l} = \tilde{p}(z^{(l)})/\tilde{q}(z^{(l)})$

MCMC (Markov Chain Monte Carlo)

Motivation

Variational Inference는 정확한 posterior 샘플링이 불가능함.

rejection sampling, importance sampling은 high-dimensional 문제에서 잘 작동하지 않음.

Idea

proposal distribution $q(z)$ 을 설정한다.
이전 샘플 $z^{(m)}$ 에 기반해 새로운 $z^{(m+1)}$ 를 생성한다.
이 과정을 반복하면, 생성된 샘플 분포가 posterior $p(z \mid x)$ 로 수렴한다.

기존 Monte Carlo는 $q(z)$ 를 고정하고 샘플링하지만,
MCMC는 $q(z)$ 를 매 스텝마다 이동시키며 적응적으로 $p(z)$ 를 근사한다.

Markov Chain

다음 상태 $z^{(m+1)}$ 는 오직 **현재 상태 $z^{(m)}$ **에만 의존한다.

$p(z^{(m+1)} \mid z^{(m)}, z^{(m-1)}, \dots, z^{(0)}) = p(z^{(m+1)} \mid z^{(m)})$

따라서 초기 확률과, 전이 확률만 있으면 모든 샘플을 만들어 낼 수 있다.

즉, $p(z)$ 를 stationary distribution으로 갖는 마르코프 체인을 만드는 것이 목표이다.

Stationary Distribution

목표: 마르코프 체인의 분포가 수렴하여 **posterior 분포 $p(z \mid x)$ **가 되는 것
$p^*(z) = \sum_{z'} T(z', z) p^*(z')$
Detailed Balance Equation:
$p^*(z) T(z, z') = p^*(z') T(z', z)$

이 조건을 만족하면 $p^*(z)$ 는 stationary 함.

수렴 조건 모든 Markov Chain이 수렴하는 것은 아니다.
수렴하려면 다음 두 조건이 필요함:
- Irreducible: 모든 상태 쌍 간 전이 가능
  $p(z^{(m)} = b \mid z^{(1)} = a) > 0$
- Aperiodic: 특정 주기 없이 상태를 다시 방문 가능
  $\gcd(m : p(z^{(m)} = a \mid z^{(1)} = a) > 0) = 1$

Metropolis-Hastings Algorithm

기본 Metropolis Proposal: 대칭 분포 $q(z^*|z) = q(z|z^*)$
$A(z^*, z^{(\tau)}) = \min\left(1, \frac{\tilde{p}(z^*)}{\tilde{p}(z^{(\tau)})}\right)$
Metropolis-Hastings (일반화된 MH)
$A_k(z^*, z^{(\tau)}) = \min\left(1, \frac{\tilde{p}(z^*) q_k(z^{(\tau)} \mid z^*)}{\tilde{p}(z^{(\tau)}) q_k(z^* \mid z^{(\tau)})}\right)$
- $q_k(z^* \mid z^{(\tau)})$ : asymmetric proposal 분포
- MH는 detailed balance를 만족하므로 $p(z)$ 로 수렴함
- 단점
  - proposal 분포의 variance가 너무 크면 → 거의 다 reject됨
  - variance가 작으면 → 샘플 이동이 느림 (convergence 느림)
  - 고차원에서는 변수마다 적절한 variance 조절이 어려움

Gibbs Sampling

각 변수에 대해 조건부 분포를 순차적으로 샘플링
특히 high-dimensional 문제에서 효과적
기본 아이디어
$p(x, y) \Rightarrow \text{직접 샘플링 어려움} \Rightarrow p(x \mid y),\; p(y \mid x) \text{ 로 분할 샘플링}$
- 항상 accept됨 (reject 없음)
- Markov blanket 기반으로 조건부 독립 구조를 활용
Markov blanket:
해당 변수의 부모 + 자식 + 자식의 부모로 구성됨

HMC (Hamiltonian Monte Carlo)

단순한 랜덤 걷기 대신, 물리 기반 운동량 정보를 이용해서 더 효율적으로 샘플링

구성 요소
- $x$ : 위치(position), $w$ : 운동량(momentum)
- 총 에너지 함수 (Hamiltonian):
$H(x, w) = U(x) + K(w)$
Hamiltonian Dynamics:

\frac{dx}{dt} = \frac{\partial H}{\partial p}, \quad \frac{dp}{dt} = -\frac{\partial H}{\partial x}

작동 방식
1. 무작위 운동량 $w_0$ 샘플링
  $p(w) \propto \exp(-V(w))$
2. Leapfrog 통합법으로 $x, w$ 를 시간 단위 $\epsilon$ 만큼 업데이트
3. MH-style accept/reject
$a(x_0, w_0, x_T, w_T) = \min\left(1, \frac{\exp(-H(x_T, w_T))}{\exp(-H(x_0, w_0))} \right)$
- 에너지가 보존되므로 accept 비율이 높음
- detailed balance 만족 → posterior 수렴 보장